gradient
- References :
- Done Reading:
- To Read:
- Questions :
In vector calculus, the gradient is a multi-variable generalization of the derivative. Whereas the ordinary derivative of a function of a single variable is a scalar-valued function, the gradient of a function of several variables is a vector-valued function
Simply, derivative of multivariable function
The gradient (or gradient vector field) of a scalar function f(x1, x2, x3, …, xn) is denoted ∇f or ∇→f where ∇ (nabla) denotes the vector differential operator, del.
\( \nabla f(p) = { \begin {bmatrix} {\frac {\partial f}{\partial x_{1}}}(p) \\ \vdots \\ {\frac {\partial f}{\partial x_{n}}}(p) \end{bmatrix}} \)
Example
\(f(x, y) = x^{2}y + y\),
\( \nabla f(x, y) = {\begin{bmatrix}{\frac {\partial f}{\partial x}}(x^{2}y + y)\\ \\ {\frac {\partial f}{\partial y}}(x^{2}y + y)\end{bmatrix}} = {\begin{bmatrix}(2xy) \\ \\ (x^{2} + 1)\end{bmatrix}} \)
Gradients and The Multivariable Chain Rule
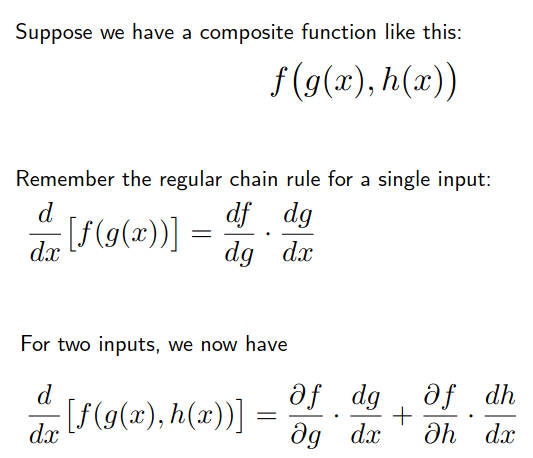
Figure 1: A example
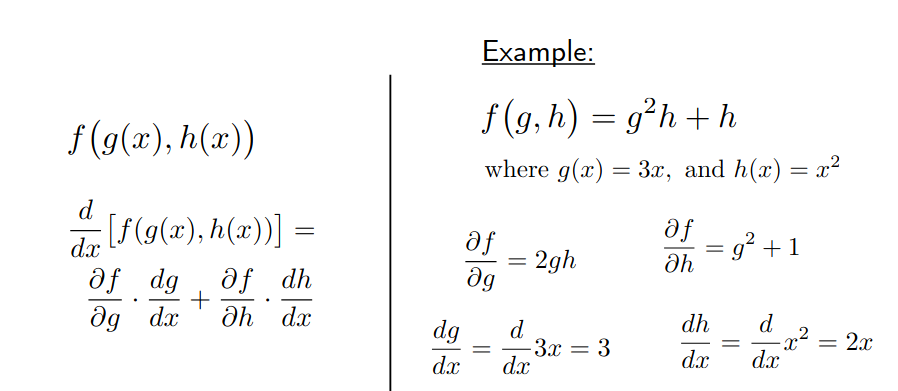
Figure 2: A example
- Result
- \( \frac{d}{dx}[f(g(x), h(x))]\ = [2gh.3] + [(g^2 + 1).2x] = 2xg^2 + 6gh + 2x \)

Figure 3: In vector form
The Jacobian Matrix

Figure 4: Jacobian Matrix