perceptron
tags:
ml
deep learning
categories:
uncategorized
References :
- Done Reading:
- Reading:
- Tom Mitchell Lectures slides of chapter 4
- Tom Mitchell, Machine Learning Chapter 4
- To Read:
Questions :
- A learning rule for the computational/mathematical neuron model
- Rosenblatt, F. (1957). The perceptron, a perceiving and recognizing automaton. Project Para. Cornell Aeronautical Laboratory
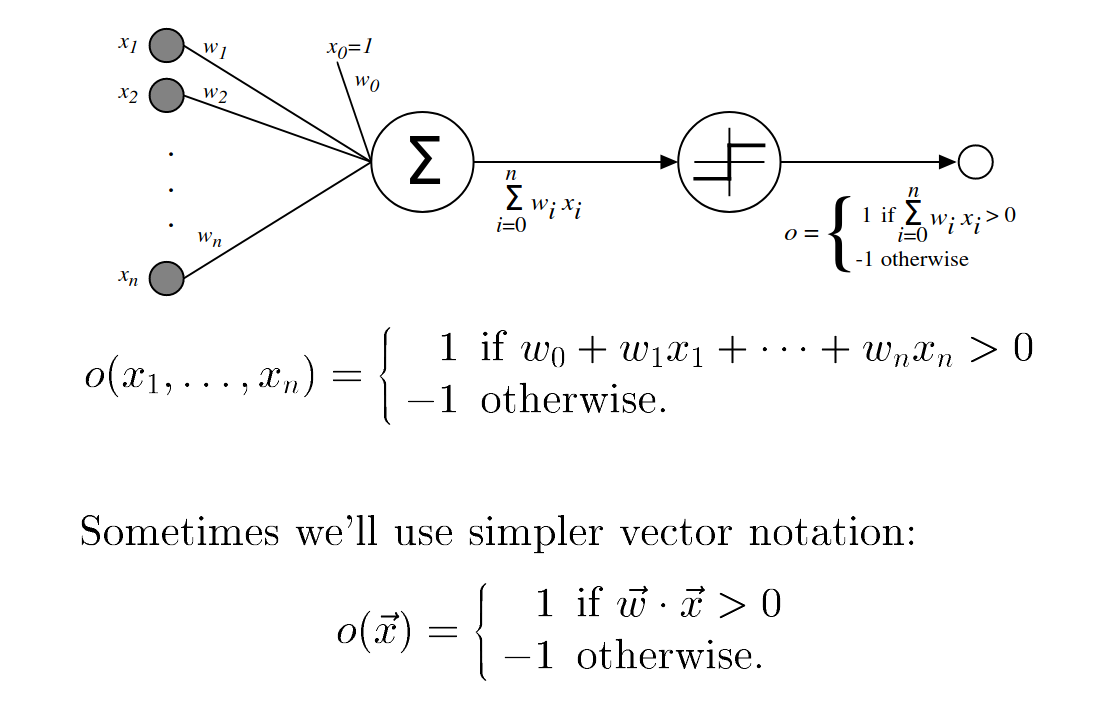
Figure 1: A perceptron
- \(o(\overrightarrow{x}) = sgn(\overrightarrow{w} \cdot \overrightarrow{x})\) where,
- \( sgn(y) = \begin{cases} 1 & \text{if y > 0} \\ -1 & \text{otherwise} \end{cases} \)
- Space \(H\) of candidate hypotheses is
- \(H = \{ \overrightarrow{w} | \overrightarrow{w} \in \Re^{n+1} \}\)
Representations
- A single layer perceptron can be used to represent many boolean functions
- AND
- \(w_{0}\) = -.8
- \(w_{1}\) = \(w_{2}\) = .5
- OR
- \(w_{0}\) = -.3
- \(w_{1}\) = \(w_{2}\) = .5
- NAND
- NOR
- AND
- However XOR function cannot be represented by a single layer perceptron
- Since the single layer cannot linearly separate the training examples
In 1969, a famous book entitled Perceptrons by Marvin Minsky and Seymour Papert showed that it was impossible for these classes of network to learn an XOR function. It is often believed (incorrectly) that they also conjectured that a similar result would hold for a multi-layer perceptron network. However, this is not true, as both Minsky and Papert already knew that multi-layer perceptrons were capable of producing an XOR function. (See the page on Perceptrons (book) for more information.) Nevertheless, the often-miscited Minsky/Papert text caused a significant decline in interest and funding of neural network research. It took ten more years until neural network research experienced a resurgence in the 1980s- Perceptron
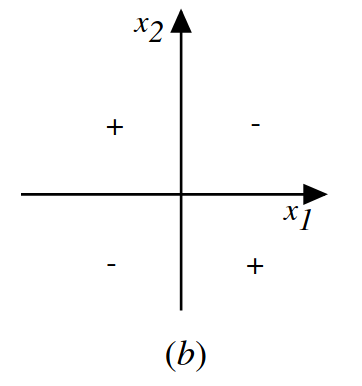
Figure 2: XOR function
Learning Rule

Figure 3: Learning Rule, from Tom Mitchell Lectures
- converges only if (gauranteed to succeed):
- the data is linearly seperable
- the \(\eta\) (eta) is sufficiently small
- Solution is Gradient Descent And the Delta Rule
Geometric Intuition

Figure 4: Geometirx Intuition, from Sebastian Raschka Lectures